La magia dei rendimenti composti

La magia dei rendimenti composti

Cosa si intende per capitalizzazione composta e quale sarebbe il suo effetto “magico”?

Cominciamo con un quiz:

Immagina di investire 1.000 euro in un titolo che frutta un tasso di interesse del 5% annuo, al netto di spese e tasse. Dopo 2 anni, quanto immagini sia la cifra disponibile ?

a) meno di 1.050 euro
b) esattamente 1.050 euro
c) oltre 1.050 euro

La risposta esatta è la c. Per la precisione, dopo due anni il capitale sarà salito a €1.102,5.

Vediamo l’evoluzione del capitale passo-passo.

Alla fine del primo anno avremo: capitale iniziale + interessi, dunque:
€1.000 + (€1.000 x 5%) = €1.000 + €50 = €1.050.
Alla fine del secondo anno avremo: capitale all’inizio del secondo anno + interessi, dunque:
€1.050 + (€1.050 x 5%) = €1.050 + €52,5 = €1.102,5.

L’aspetto importante da sottolineare è che nel secondo anno abbiamo maturato più interessi che nel primo, perché oltre agli interessi sul capitale iniziale, abbiamo maturato anche interessi sugli interessi maturati nel primo anno, insomma un guadagno sui guadagni. Questo è il principio della capitalizzazione degli interessi. Più passa il tempo, più la capitalizzazione degli interessi accelera la crescita del capitale. Grazie alla capitalizzazione, 1.000 euro investiti al 5% netto all’anno diventano 1.630 (anziché 1.500) dopo 10 anni, ben 2.650 dopo 20 anni e oltre 4.320 dopo 30 anni. In quest’ultimo caso, addirittura, gli interessi sugli interessi sono superiori agli interessi sul capitale!

Su periodi lunghi anche le piccole cifre diventano importanti.

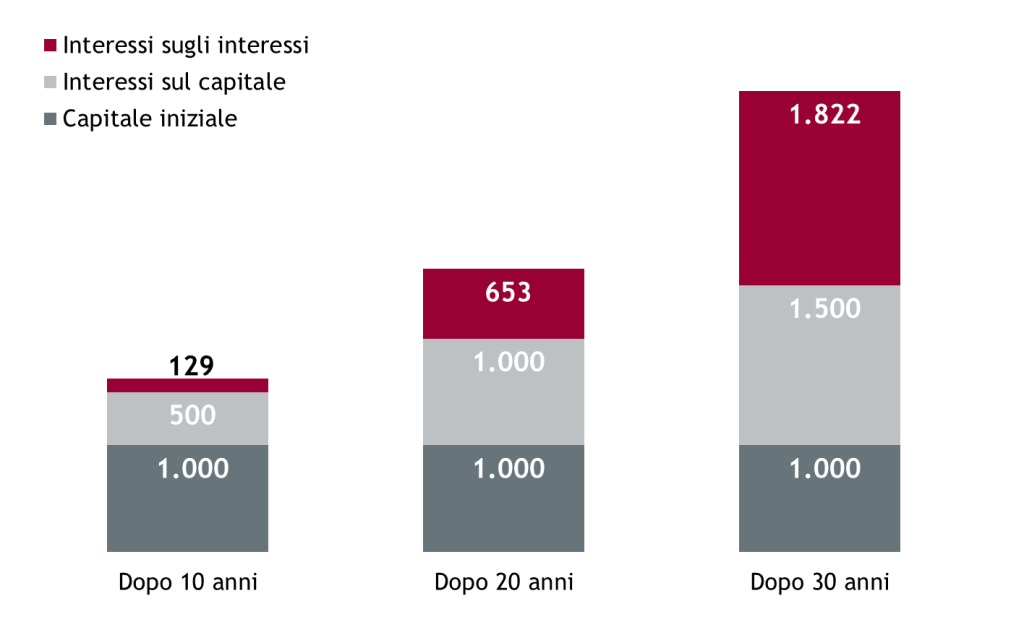
Più dei numeri conta il fatto che pochi euro al giorno o al mese, moltiplicati per molti giorni e con il “tocco magico” della capitalizzazione composta degli interessi, possono trasformarsi in cifre importanti.

Gli effetti moltiplicatori della capitalizzazione composta degli interessi, in particolare, si fanno sempre più decisivi man mano che si allunga il periodo dell’accumulazione del risparmio.